| | |
|
 组别 组别 | 限制发言用户 |
 级别 级别 | 大将军 |
 好贴 好贴 | 6 |
 功绩 功绩 | 517 |
 帖子 帖子 | 11552 |
 编号 编号 | 1037 |
 注册 注册 | 2004-10-25 |
 来自 来自 | 天津 |
 家族 家族 | 司徒实业 |
| |
| | |
|
|
|
|
浅议庞加莱猜想
最近大家在射虎,茶馆等区都看到了,有关我国科学家朱熹平和曹怀东突破百年难题的帖子。该研究成果并且被哈佛大学教授,著名华裔数学家,费尔茨奖章得主,丘成桐教授所认同。在美国出版的《亚洲数学期刊》6月号以专刊的方式,刊载了长达300多页、题为《庞加莱猜想暨几何化猜想的完全证明:汉密尔顿-佩雷尔曼理论的应用》的长篇论文。从去年9月底至今年3月,朱熹平和曹怀东应邀前往哈佛大学,以每星期3小时的时间——连续20多个星期、共约70个小时——向包括哈佛大学数学系主任在内的5位数学家进行讲解,回答了专家们提出的一系列问题。此证明并且在6.19 - 6.24北京的世界级弦理论大会上向全球公开,一时在各界引起了轰动。那么下面让我先用通俗的语言,介绍一下此猜想的历史和背景。另外,还对会弦理论做一个简单的介绍,最终目标是希望能把这两个概念连接起来。最后,我们也可以讨论一下该猜想严格定义,以及“它具体为什么那么难”?Hamilton, Perelman, Zhu/Cao 他们之间的工作到底有什么不同?具体又都是贡献了哪一部分呢?
一,介绍
在进入深入探讨之前,先介绍一下命题:任何一个封闭的三维流形,只要它里面所有的封闭曲线都可以收缩成一点,这个空间就一定是一个三维圆球--这就是法国数学家庞加莱于1904年提出的猜想。
下面我们探讨一下这个猜想到底是什么意思。首先,我们可以把流形想象成任何一个光滑的曲面。那么在一些曲面上,我们可以随便画一条曲线,最后把该线的头和尾都连接起来形成一个圈。对于这个圈,我们可以牵着线头来把它拉小,甚至把它拉小到只剩下一个点。关于这个特征,我们称之为“简单联接”(simply connected)。但比如在另一些区面上,这个特征就不能实现,例如 T = 一个面包圈(左图)
 
它的表面是光滑的,所以我们可以理解它属于流形的一种。但如果我们横腰画一条线,让这条线缠着面包圈走,那么只要缠的总次数 >= 1,该线就无法被收缩成一个点(除非把面包圈切断)。但如果流形本身是个球(右图),或者是个平面,那么我们不难想像“简单连接”的这个特征还是可以满足的。从通俗的角度上看,此特征的唯一可能失败的理由,就是如果流形本身有很多的洞,例如面包圈中间那个孔,或者如同克兰瓶中间的那个洞。(图)这里提到的“洞数”,如果把它严格化了之后,就是一个流形的“欧拉特征”。它在拓扑学中是一个区分不同类型曲面的重要工具。

下面,我们为了排除无穷大有可能给我们的一些麻烦,我们将假设所有的流形都有封闭性(compact)。所谓封闭性大体上讲,它的意思就是存在一个足够大的箱子,使得我们的流形可以完全装在该箱子里面。那么从这个角度上看,平面这个情况就被删除了,因为平面是无限的。我们的直觉告诉我们,球体是唯一的一种封闭的流形,满足“简单连接”性的可能。那么事实是否如此呢?这个问题就是困惑了数学界整整100年的庞家莱猜想!
这里还要声明一下,为了让大家理解着方面,我举的例子全都是用三维空间里的二维流形,庞猜想在这种情况并不难证明。几何学在十九世纪末发生了翻天覆地的变动。以黎曼为首的一些新学派,认为没有必要假设一个曲面,就一定要被另一个更高维平面空间(欧氏空间)所包含。曲面本身应该是一个独立的个体,而当我们说这个曲面是三维的时候,我们实际的意思是它的切面是一个三维空间(流形就是靠这个特征定义的),而一个普通三维空间里的曲面,它的切面则是二维的。希望以后写“三维曲面”的时候,举的二维曲面的例子不会误导大家。
也许一些朋友对庞加莱猜想的背景有些了解,庞加莱最初的猜想是:任意维的封闭流形,如果它有“简单联接”的特征,那么它一定可以在“不被撕破”的情况下,被“捏”成一个N维空间的球体(i.e. homeomorphic to N-sphere)。这个命题当N = 1的时候,情况显然,因为曲线和流形之间完全没区别。N=2的情况,庞加莱自己在写出了猜想前,就已经证明出来了。或者说,也许是N=2这个例子让他联想到,更高的 N 该结果是否也能成立。N > 5 的情况在50年代被解除,N = 4 随后不久也被解答。那么问题是为什么单单在 N = 3 的时候,该猜想那么难呢?这个原因还在于“简单联接”的定义,是用一个一维曲线来测量连接性。而一维曲线本身,又恰恰只有在三维空间里才可以打结(左图)。

在二维空间,因为空间太小,不能打结。如果去四维空间以上,那么因为空间太大,打出来的任何结都可以被轻松松开。只有三维空间,我们才能用一维空间的曲线来做结。当然现代结理论中,已经深入到了看怎么用 M 维曲面在一个 N 维流形中做结。我个人的一个猜想,数学界里给“homeomorphism(拓扑曲面等价条件)”做定义的时候,应该是19世纪末。当时应该并没有把结的问题考虑进去,而结理论一直到20世纪才开始有了一些初步的发展。这个问题在庞猜想的难度问题上,体现得很明显。
庞加莱猜想和黎曼猜想、霍奇猜想、杨振宁/米尔理论等一样,被并列为七大数学世纪难题之一。2000年5月,美国的克莱数学研究所为每道题悬赏百万美元求解。
二。拓扑学的基本介绍
在第一部分,我们了解了庞猜想的一个轮廓,那么它在整个数学界到底起到了一个什么作用呢?说到这里,我们就不得不简单的介绍一下拓扑学到底是在研究一些什么样的东西了。简单的说,拓扑就是“橡皮筋版的几何”。在几何中,所有的东西都是硬邦邦的,我们不能把直线折弯,我们不能随便把圆的说成方的,等等。但在实际应用中,我们却经常发现几何学总体来说“太硬”了,把很多非常简单的原理,不必要的复杂化。
我们先看一些现实生活中的例子,如果谁是短发的话,请你摸摸自己的后脑勺,是否发现有一个旋?如果你是长发的话,也许你的手续要沿着头发根摸,但这个旋还是可以摸到的。也许很多人会认为,人体的基因控制头发这么长,但其实这就是一个典型的数学问题。如果你不信,你可以随便拿一个球,把球上粘满了毛,看看你有没有什么办法能让旋不出现?这里又涉及到了拓扑问题,如果你拿一个球,那么无论你怎么梳理,球上的毛永远会出现旋的。但如果你拿一个面包圈,那么你可以把所有的毛都梳向一个方向,梳一圈最终还是可以梳回来的。这样就可以保证不出现任何旋。为什么我说这个是拓扑问题呢?因为无论是面包圈还是球,只要不撕破的情况下,无论你怎么捏它,让它变形,最终能否在它身上粘满无旋的毛发,这个问题的结果都不会改变的。
再举一个更简单的例子,大家每天睡醒,从自己的床上爬起来出门,我们是通过什么找到门的位置呢?按几何学的理解,我们应该有一个行进的角度,加上一个行进距离,只要这两个参数不出问题,那么我们就可以从门走出去。但实际生活中,我们并不需要计算这两个参数,就可以轻松得找到门的位置。因为门的拓扑特征和墙的其他部位不一样,门的位置有个洞,别处没有。不管门的形状是方的还是圆的,我们所找的就是墙上有洞的位置。这个特征在工程学中也经常用到,一些现代的 drones 和小型机器人,在室外可以靠GPS,但在室内一般就是用拓扑特征来分辨自己的位置。
从上面的两个例子上看,拓扑学主要解决的是形状的基本特征。两个形状之间,如果存在一个连续变幻,使得一个形状可以变成另外一个,那么这两个形状就是等价的 (homeomorphic)。例如,一个圆形和一个方块,我们可以给圆形一个解析方程:
|x|^2 + |y|^2 = 1

对于一个正方形,我们也可以给出一个解析方程: |x| + |y| = 1 (它的形状是把(0,1), (1,0), (0,-1)和(-1,0)四个点用直线连接起来的正方形). 从这个角度看,把一个圆形连续地变成一个方块,我们可以通过
|x|^a + |y|^a = 1
里面的参数 a, 把它从 2 逐渐地变换为 1。那么画成图我们就会看到那个圆逐渐的缩为顶点为(0,1), (1,0), (0,-1)和(-1,0)的正方形。这个等价定义看似非常自然,但它本身也有所谓的遗漏,这就是我以前说过的结现象。从连续性的角度上看,一个结何一个圆是没有任何区别的,但是我们很难想象怎么在不切不剪的情况下,完成这个转换。
 
我们假设一只蚂蚁,围着我们的结跑一圈需要的时间是1. 也就是说,如果令 phi(t) 为蚂蚁在 t 时刻的位置,那么有 phi(0) = phi (1) = 起点/终点。其中当 t 从 0 连续变换成 1 的时候,我们的蚂蚁也连续地围着结绕了一圈。这说明,函数 phi: [0,1] ---> 结 是一个连续函数。这时候,我们假设一只蜗牛在一个复平面上,在同样的时间 t,它的位置是 psi(t) = e^(it) = cos(t) + i sin(t)。显然,psi(t) : [0,1] ---> 圆 也是一个连续函数。由于连续函数的逆函数是连续的,并且连续函数的叠加出来也是连续的,因此
F(x) = (phi o psi^(-1) ) (x)
是一个 F: 圆 ---> 结 的连续函数;其中 x 是圆上的任意元素,o 是函数叠加,psi^(-1)是 psi 的逆函数。由拓扑等价定义(homeomorphism),两者之间只要存在一个连续映射,那么它们就是等价的。因此,由于 F 的存在,一个结和一个圆,在拓扑上是没有区别的。
从上面的例子上看,仅仅把拓扑等价,理解为“在不撕破的情况下,可以把一个形状捏成另外一个形状”,其实是不准确的。但作为初学者,这么理解在大多数的情况还是没什么问题的,只是注意有时候会有反例出现就是了。那么下面我们讨论一下连续性在拓扑中到底是一个什么角色?拓扑的严格定义又是什么呢?
定义:一个拓扑空间就是一对集合:(X, O),X 里的元素为拓扑空间的点,而 O 里的元素皆为 X 的子集,这些子集我们称之为“开集”。开集需要满足以下公理:
1。{X}, {空集} 皆开。
2。如果 A, B 是开集,那么 A U B 也是开集。
例如:X = {0,1,2}, O = {{空集}, {0}, {1}, {0, 1}, {0,1,2}}, 那么(X, O)就是一个拓扑空间。
定义:如果一个集合的反集是开集,那么我们称之为闭集。
定义:令(X, O), (Y, P)为两个拓扑空间,如果函数 f: X ---> Y,满足:对于每一个 Y 的开集 y, 集合 x = {u in X : f(u) in y} 也是开集。那么我们称 f 为一个连续函数。
换句话说,所谓连续函数是能保护拓扑结构的函数,而拓扑结构无非是一些我们“宣布”为开集的集合。另外,连续函数也受到拓扑结构的限制,一般来说,取值域的拓扑结构越细腻,f 就越容易是连续的。比如说,如果我们令 f: R_1 ---> R_2 ,f(x) = x,其中 R_1, R_2 都是实数。R_1 的拓扑结构 O_1 是由(a,b)这种开段来构成的, R_2 的拓扑结构 O_2 是实数的所有子集和。由于有理数集在 O_2 是开集,但在 O_1 不算开集,那么f(x) = x 在这个情况下就不是一个连续函数(经管画图看起来很连续)!如果我们反过来,考虑 f : R_2 ---> R_1,那么即便令 f(x) = I_Q (x) (I_Q (x) = 1 如果 x 是有理数,=0 如果 x 是无理数),一个看起来很不连续的函数,在这个拓扑环境下它也是连续的。
从公理上看,拓扑结构目前不需要有人和几何意义,但拓扑结构在几何学中的应用是不可忽略的。因此,为了避免上面描述的一些“坏例子”,我们只考虑流形的拓扑特征。在19世纪莫,庞加莱等数学家们把二维封闭流形分为四种情况:
1。圆,2。面包圈,3。克兰瓶,4。投射面。图片按顺序如下:
他还证明了,任意二维流形都可以写成这四种基本流星的“和”。例如,
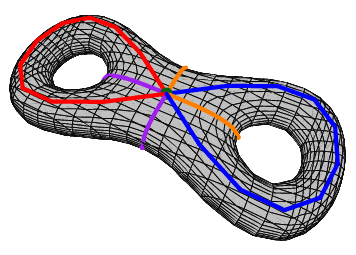
可以想成是两个面包圈的和。
(填坑中)
三。80年代的发展: Ricci flows.
(填坑中)
四。Perelman 的贡献。
(填坑中)
五。曹/朱的贡献
(填坑中)
六。和弦理论的关系
最后简单的说说该猜想和弦理论有什么关系。大体上说,在理论物理界中,有适合于微观世界的量子论和适合于宏观世界的广义相对论。这两个理论目前不容和,其中最不融合的就是引力部分。而如果我们要硬把他们放到一起的话,那么我们就会得出一些匪夷所思的计算预测,例如 Pr(某事件)= sqrt(-1),两个引力子之间的作用力是无穷大,等等。所谓弦理论就是为了修饰这两者之间的不容和性。简单的说,弦理论假设了宇宙的最小单元是一根弦,而不是我们以前看到的电子/光子一类的点。这根弦是一个十维空间的物体,其中有三维空间是张性的,还有六维是结性的(knotted dimension)。这六维结性空间所产生的流形,我们称之为Calabi-Yau流形。其中华裔数学家丘成桐(Shing-Tung Yau),就是此理论的奠基人之一。在弦理论中,在四大基本力中,只有引力子是一个关闭弦(G-String)。另外三种力的信号粒子:光子(E-String),强力子(S-String)和弱力子(W-String),都是以开弦的形式出现。我们现在所感兴趣的,引力子,就是一个关闭弦。而庞猜想告诉了我们,如何通过分析关闭弦的特征,来推出流行的宏观特征。换句话说,也许庞猜想的成立,是为我们以后探讨宇宙形状的一个里程碑!
(填坑中)
Appendix:数学上的严格定义
[ 本帖最后由 天宫公主 于 2006-6-30 18:01 编辑 ]
|

|
|
|
|