Board logo

标题: A*寻路算法与它的速度 [打印本页]
作者: lufy    时间: 2010-7-14 12:10     标题: A*寻路算法与它的速度

A*算法与它的速度

如果你是一个游戏开发者，或者开发过一些关于人工智能的游戏，你一定知道A*算法，如果没有接触过此类的东东，那么看了这一篇文章，你会对A*算法从不知道变得了解，从了解变得理解。
我不是一个纯粹的游戏开发者，我只是因为喜欢而研究，因为兴趣而开发，从一些很小的游戏开始，直到接触到了寻路等人工智能，才开始查找一些关于寻路方面的文章，从而知道了A*算法，因为对于初期了解的我这个算法比较复杂，开始只是copy而已，现在我们一起来精密的研究一下A*算法，以及提高它的速度的方法。

一，A*算法原理

我看过Panic翻译的国外高手Patrick Lester的一篇关于A*算法初探的文章，现在我就根据回忆，来慢慢认识A*算法的原理。
我们先来看一张图

图中从起点到终点，需要绕过一些遮挡，也许我们看的比较简单，但是实际上，交给电脑来实现却要经过一番周折，电脑如何知道哪里有遮挡物，又是如何找到从起点到终点的最短路径的呢？
了解这些，我们首先要知道一个公式：
F = G + H
其中，F 是从起点经过该点到终点的总路程，G 为起点到该点的“已走路程”，H 为该点到终点的“预计路程”。
A*算法，要从起点开始，按照它的算法，逐步查找，直到找到终点。
初期，地图上的节点都是未开启也未关闭的初始状态，我们每检测一个节点，就要开启一些节点，检测完之后，要把检测完的节点，就要把它关闭。
我们需要一个开启列表和关闭列表，用来储存已经被开启的节点和被关闭的节点。
这些就让我们在实际过程中来深入了解吧。
看下面的图

首先，我们来从起点出发，开启它周围的所有点，因为遮挡是无法通过的，我们不去管它，这样，被我们开启的节点，就是图中的三个节点，它们的父节点就是起点，所以图中的箭头指向起点，计算相应的FGH值，如图所视，检测完毕，将起点放入关闭列表。
这个时候，我们从被开启的所有节点中查找F值最小的节点，做为下一次检测的节点，然后开启它周围的点。
这时候起点左方和下方的F值都是70，我们根据自己的喜好选择任意一个，这里先选择下方的节点进行检测。
如下图

首先把未被开启的剩下的节点的父节点指向检测点。
已经开启的点，我们不去开启第二遍，但是我们计算一下从检测点到达它们的新的G值是否更小，如果更小则代表目前的路径是最优的路径，那么把这个节点的父节点改为目前的检测点，并重新计算这个点的FGH的值，全部检测完毕之后，关闭检测点，然后开始寻找下一个节点，如此循环，直到找到终点。
然后从终点开始，按照每个节点的父节点，倒着画出路径，如下图

这个就是A*算法的原理，说难倒是不难，但是对于初步接触的人来说有点费劲而已。

二，A*算法的速度

前面，我们了解了A*算法的原理，发现，在每次查找最小节点的时候，我们需要在开启列表中查找F值最小的节点，研究A*的速度，这里就是关键，如何更快的找出这个最小节点呢？

1，普通查找算法

我们先来看看，最简单的做法，就是每次都把开启列表中所有节点检测一遍，从而找到最小节点
private function getMin():uint {
        var len:uint = _open.length;
        var min:Object = new Object();
        min.value_f = 100000;
        min.i = 0;
        for (var i:uint = 0; i<len; i++) {
                if (min.value_f>_open.value_f) {
                        min.value_f = _open.value_f;
                        min.i = i;
                }
        }
        return min.i;
}
这里我用了一张很简单的地图来验证此方法
运行结果如图

我们看到，耗时38毫秒，其实这个数字是不准确的，我们权且当作参考

2，排序查找算法

顾名思义，这个算法就是，始终维持开启列表的排序，从小到大，或者从大到小，这样当我们查找最小值时，只需要把第一个节点取出来就行了
维持列表的排序，方法是在太多了，我的方法也许很笨，勉强参考一下吧，我们每次排序的同时，顺便计算列表中的平均值，这样插入新节点的时候，根据这个平均值来判断从前面开始判断还是从后面开始判断

//加入开放列表
private function setOpen(newNode:Object):void {
        newNode.open = true;
        var __len:int = _open.length;
        if (__len==0) {
                _open.push(newNode);
                _aveOpen = newNode.value_f;
        }else {
                //和F平均值做比较，决定从前面或者后面开始判断
                if (newNode.value_f<=_aveOpen) {
                        for (var i:int=0; i<__len; i++) {
                                //找到比F值小的值，就插在此值之前
                                if (newNode.value_f<=_open.value_f) {
                                        _open.splice(i, 0, newNode);
                                        break;
                                }
                        }
                } else {
                        for (var j:int=__len; j>0; j--) {
                                //找到比F值大的值，就插在此值之前
                                if (newNode.value_f>=_open[(j-1)].value_f) {
                                        _open.splice(j, 0, newNode);
                                        break;
                                }
                        }
                }
                //计算开放列表中F平均值
                _aveOpen += (newNode.value_f-_aveOpen)/_open.length;
        }
}
//取开放列表里的最小值
private function getOpen():Object {
        var __next:Object =  _open.splice(0,1)[0];
        //计算开放列表中F平均值
        _aveOpen += (_aveOpen-__next.value_f)/_open.length;
        return __next;
}
运行结果如图

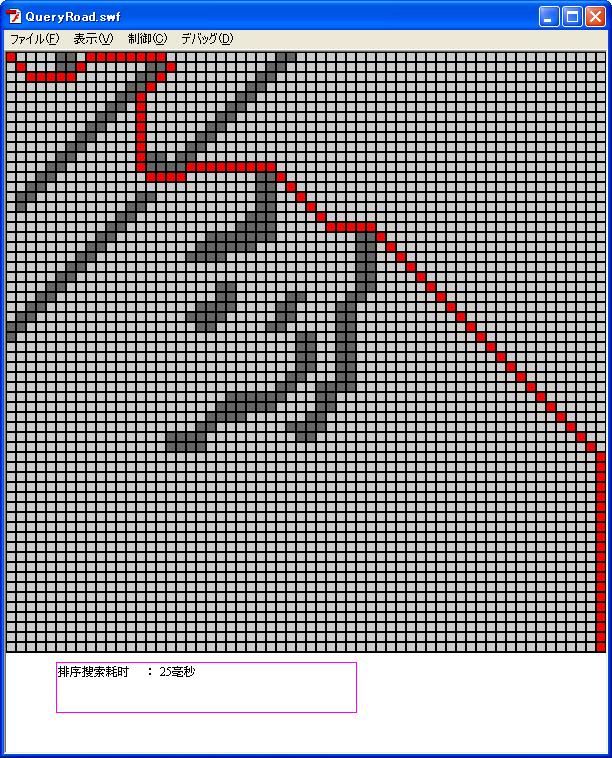
我们看到，耗时25毫秒，这个数字虽然不准确的，但是与普通查找算法相比较，速度确实是提高了

3，二叉树查找算法
(参考了火夜风舞的C++新霖花园中的文章)
这个算法可以说是A*算法的黄金搭档，也是被称为苛求速度的binary heap”的方法
就是根据二叉树原理，来维持开启列表的“排序”，这里说的排序只是遵循二叉树的原理的排序而已，即父节点永远比子节点小,就像下面这样
   1
|    |
5    9
|   |  |
7  12 10
二叉树每个节点的父节点下标 = n / 2;(小数去掉)
二叉树每个节点的左子节点下标 = n * 2;右子节点下标 = n * 2 +1
注意，这里的下标和它的值是两个概念
//加入开放列表
private function setOpen(newNode:Object,newFlg:Boolean = false):void {
        var new_index:int;
        if(newFlg){
                newNode.open = true;
                var new_f:int = newNode.value_f;
                _open.push(newNode);
                new_index = _open.length - 1;
        }else{
                new_index = newNode.index;
        }
        while(true){
                //找到父节点
                var f_note_index:int = new_index/2;
                if(f_note_index > 0){
                        //如果父节点的F值较大，则与父节点交换
                        if(_open[new_index].value_f < _open[f_note_index].value_f){
                                var obj_note:Object = _open[f_note_index];
                                _open[f_note_index] = _open[new_index];
                                _open[new_index] = obj_note;
                                                               
                                _open[f_note_index].index = f_note_index;
                                _open[new_index].index = new_index;
                                new_index = f_note_index;
                        }else{
                                break;
                        }
                }else{
                        break;
                }
        }
}
//取开放列表里的最小值
private function getOpen():Object {
        if(_open.length <= 1){
                return null;
        }
        var change_note:Object;
        //将第一个节点，即F值最小的节点取出，最后返回
        var obj_note:Object = _open[1];
        _open[1] = _open[_open.length - 1];
        _open.pop();
        _open[1].index = 1;
        var this_index:int = 1;
        while(true){
                var left_index:int = this_index * 2;
                var right_index:int = this_index * 2 + 1;
                if(left_index >= _open.length){
                        break;
                }else if(left_index == _open.length - 1){
                        //当二叉树只存在左节点时，比较左节点和父节点的F值，若父节点较大，则交换
                        if(_open[this_index].value_f > _open[left_index].value_f){
                                change_note = _open[left_index];
                                _open[left_index] = _open[this_index];
                                _open[this_index] = change_note;
                                                               
                                _open[left_index].index = left_index;
                                _open[this_index].index = this_index;
                                                               
                                this_index = left_index;
                        }else{
                                break;
                        }
                }else if(right_index < _open.length){
                        //找到左节点和右节点中的较小者
                        if(_open[left_index].value_f <= _open[right_index].value_f){
                                //比较左节点和父节点的F值，若父节点较大，则交换
                                if(_open[this_index].value_f > _open[left_index].value_f){
                                        change_note = _open[left_index];
                                        _open[left_index] = _open[this_index];
                                        _open[this_index] = change_note;
                                                                       
                                        _open[left_index].index = left_index;
                                        _open[this_index].index = this_index;
                                                                       
                                        this_index = left_index;
                                }else{
                                        break;
                                }
                        }else{
                                //比较右节点和父节点的F值，若父节点较大，则交换
                                if(_open[this_index].value_f > _open[right_index].value_f){
                                        change_note = _open[right_index];
                                        _open[right_index] = _open[this_index];
                                        _open[this_index] = change_note;
                                                                       
                                        _open[right_index].index = right_index;
                                        _open[this_index].index = this_index;
                                                                       
                                        this_index = right_index;
                                }else{
                                        break;
                                }
                        }
                }
        }
        return obj_note;
}
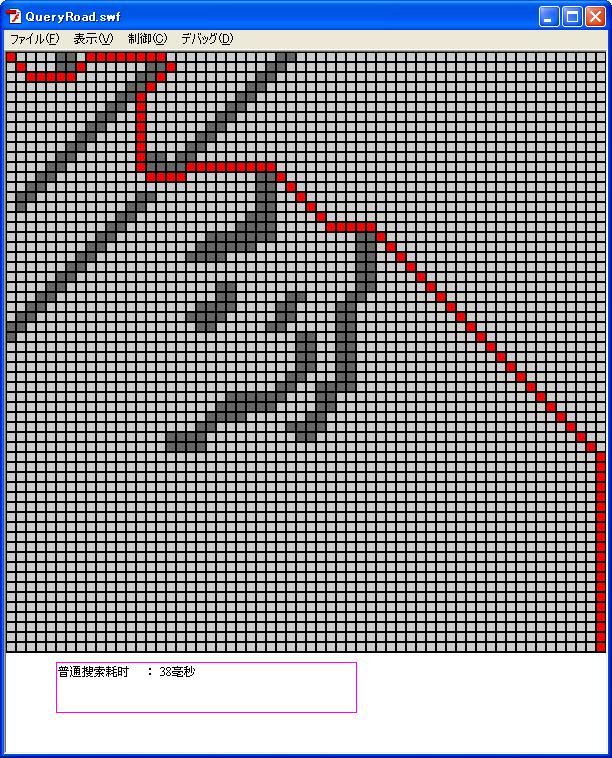
运行结果如图

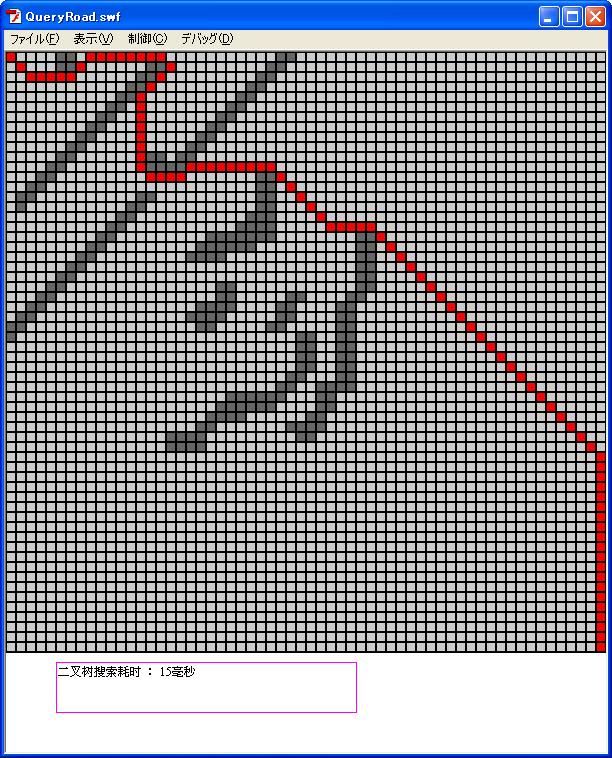
我们看到，耗时15毫秒，速度是这三个方法里最快的，但是因为这个数字是不够准确的，实际上，用二叉树查找法，会让A*算法的速度提高几倍到10几倍，在一些足够复杂的地图里，这个速度是成指数成长的。

4，总结
得出结论，用了A*算法，就要配套的用它的黄金搭档，二叉树，它可以让你的游戏由完美走向更完美。

[ 本帖最后由 lufy 于 2010-8-6 12:59 编辑 ]
作者: 司徒苍月    时间: 2010-7-14 12:14

直接说 寻路算法 更通俗些
作者: lufy    时间: 2010-7-14 12:22

说的是，改
作者: 周瑜    时间: 2010-7-14 19:52

大致看了一下，这个A*算法其实就是Dijkstra算法，而最后的二叉树查找算法应该改名叫堆排序算法更准确一些。
作者: tydea    时间: 2010-7-16 10:13

虽然不懂，但还是顶顶
作者: 将来的mod达人    时间: 2010-7-26 20:41

我想知道LZ的意图。。。。是想研究曹操传AI的行走路径= =？
作者: 陈珺    时间: 2010-8-3 00:05

A*是广度优先，做很多无用功，为了保证精确，把各种可能都比较过去，非常耗时
作者: 《苍狼白鹿传》    时间: 2010-8-5 17:13

假设从（0,0）到（40,40）有1600个单位，假设每单位有三个值 0 可移动 1不可移动 2已经移动过
首先可移动只有两个方向（算正方向，斜向算两步）
然后对四个方向编号，1上 2左 3下 4右，运动路径就被一串数字记录
当前坐标 2字节
先计算横纵坐标差值之和，就是走三角形两条直角边的距离
然后以这个距离作为最小值
横轴优先纵轴其次，先测试能否直接通过直角边到达


遇到障碍然后转变方向，只有两个选择 向上 向下  
向上的话距离在增加，所以优先的还是向下，上一个单位优先测试向右（注意最开始不可能回头的）

比方达到（25,0）的时候，（26,0）是障碍
那么就尝试往（25,1）走遇到障碍尽量往目的地最近的点靠近



像这样的走直线在RPG中比较常见，然后遇到障碍物停住的现象也有

[ 本帖最后由 《苍狼白鹿传》 于 2010-8-5 17:19 编辑 ]
作者: 《苍狼白鹿传》    时间: 2010-8-5 17:24

当然被障碍物卡住只能说明AI太弱智

一般最优先的假设就是没有障碍

每一步都检测最靠近的走法

O  A
A  X   就想这样从（0，0）到（40，40）只有这两个方向是接近的，所以优先考虑着两个方向
O是假设弟N步所在 A是N+1步的CASE

内存存储空间比较多
第一步就有两个CASE 所以到障碍物之前就有2的N次方作为存储空间
但是 3 4 和 4 3是同样的结果，先下后右 先右后下
所以每一步方向记录的数字会对比， 那么34443和33444是一样的最后只统计每个数字的个数

如果到了死角
O A B
A B X
B X X   B是障碍 A是预计的下一步，那么经过两个case以后返回结果是进入死角
这时候开始返回
返回也是先横坐标再纵坐标

不论向左还是向上都可以算远离了目标
所以在这种情况下马上继续按照最近原则找

考虑不回头原则

那么路径有可能是

A----
      |    X
      |  X
   C-BX
   | X
   D

A-D

这样的测试是优先横坐标

比方从 0 0 到 5 5
有一排障碍
AOOOX
OOOXO
OOXOO
OXOOO
OOOOB
优先走到 3 0（准确的说还只是测试，不是真的走）
两个方向不能走，不能回头
然后在 2 0 拐弯
因为从 2 0 到 2 1 和到3 0 效果一样
但是优先横坐标

到了2 1 又被卡死 然后左走（最后1234四个方向相加减得出最近的结果）

这时候到了 1 1 ，优先考虑往最近方向 向下 到了1 2 于是根据这个原则，一直走到0 4然后又回到最初原则，横坐标
这样的话实际路程是11 而最近是8
这时候尝试缩减路程

最明显的是 A B
                D C这样的路径直接变成 A
                                                 B
但是像
O O O
X X O
O O O
的路径可能难以发现
这时候就尝试变换横纵坐标走法
比方3 4 变成4 3

于是可以变成
O O X
X O O
O O O
这就缩短为

O O X
X O X
O O X
利用循环从开始到最后变换以后测试（前提是不撞上障碍）

实际上也有些路径计算就想这样 的，比方贴着墙走，然后走到了门口进去

[ 本帖最后由 《苍狼白鹿传》 于 2010-8-5 17:44 编辑 ]
作者: 墨叶    时间: 2010-8-5 17:49

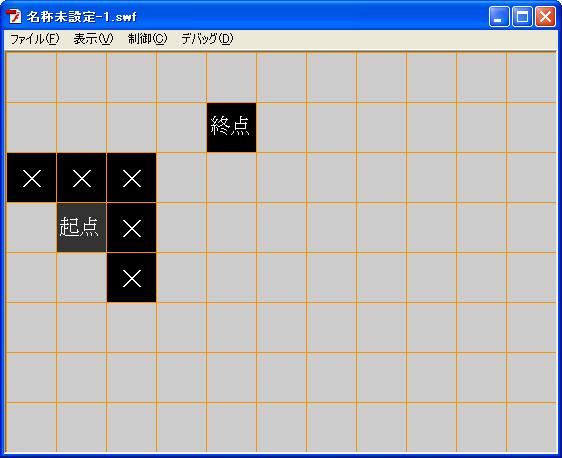
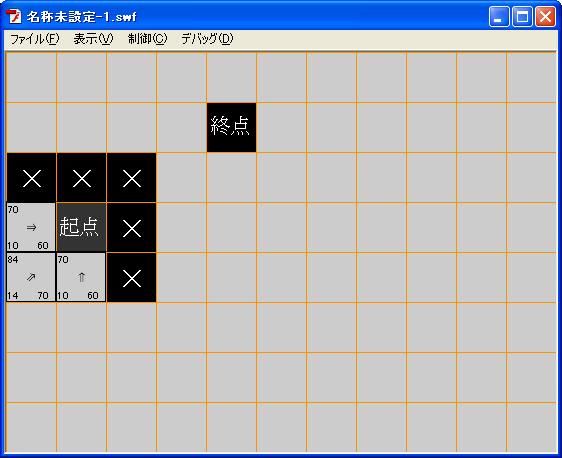
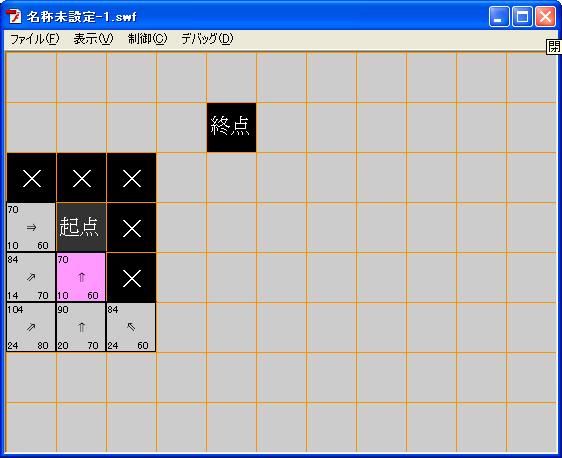
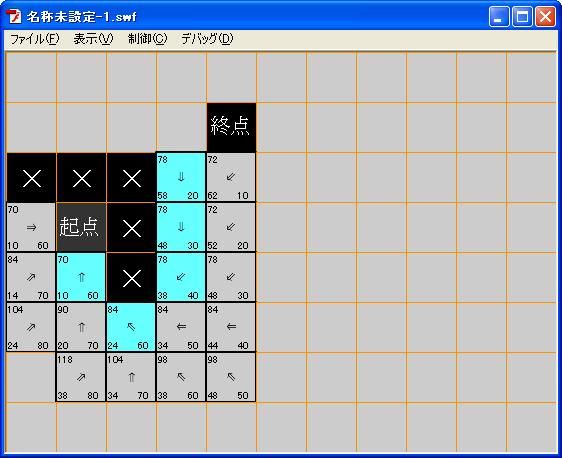
疑问：对图1，最佳路线为下，右下，右上，上，上，上。总路程为72。
小于78。
作者: 《苍狼白鹿传》    时间: 2010-8-5 17:53

图挂了？不知道怎么回事都没看到
作者: lufy    时间: 2010-8-6 13:04     标题: 回复 #10 墨叶 的帖子

看得真仔细阿，图是偷懒手动计算画出来的，一不小心画错了，改了一下，哈哈，非常感谢
作者: northwind_x    时间: 2010-8-12 12:52

楼主图挂了……
作者: lym20    时间: 2010-8-14 09:52

还是不懂
作者: jakerl    时间: 2010-9-9 10:22

这是普通的Dynamic programming算法，会有curse of dimensionality
作者: 513633522    时间: 2010-12-3 11:08

路飞好厉害啊，高手，能否给个联系方式，向路飞学习下ActionScript 3.0
作者: lufy    时间: 2010-12-3 11:26



QUOTE:
原帖由 513633522 于 2010-12-3 11:08 发表
路飞好厉害啊，高手，能否给个联系方式，向路飞学习下ActionScript 3.0

我也不过是个初学者阿，高手可谈不上
一切都在学习中学习中......



欢迎光临 轩辕春秋文化论坛 (http://xycq.org.cn/forum/) Powered by Discuz! 5.0.0